软考

发布日期: 2023-04-18

计算机组成与体系

1.1 数据的表示

1.1.1、进制转换

1.1.1.2、二进制转十进制

将二进制数转换为十进制数，可以使用加权法。具体做法是将每一位的值乘以2的对应幂次方，再将得到的结果相加即可。

例如，将10001001转换为十进制：

1 * 2^7 + 0 * 2^6 + 0 * 2^5 + 0 * 2^4 + 1 * 2^3 + 0 * 2^2 + 0 * 2^1 + 1 * 2^0 = 128 + 8 + 1 = 137

因此，10001001的二进制表示是十进制数137。

1.1.1.2 十进制转二进制

使用短除法

短除法是一种将十进制数转换为二进制数的方法，其基本原理是将待转换的十进制数不断除以2，得到的余数按相反顺序排列就是转换后的二进制数。以下是一个例子：

将十进制数137转换为二进制数。

137 / 2 = 68 ... 1
 68 / 2 = 34 ... 0
 34 / 2 = 17 ... 0
 17 / 2 =  8 ... 1
  8 / 2 =  4 ... 0
  4 / 2 =  2 ... 0
  2 / 2 =  1 ... 0
  1 / 2 =  0 ... 1

将上述除法中每一步得到的余数按照下面的方法组成二进制数，即可得到十进制数137的二进制表示：

137 =   1 * 2^7
     + 0 * 2^6
     + 0 * 2^5
     + 0 * 2^4
     + 1 * 2^3
     + 0 * 2^2
     + 0 * 2^1
     + 1 * 2^0

因此，十进制数137的二进制表示为10001001。在这个二进制数中，第一个数位是该数的最高位（即2^7），最后一个数位是该数的最低位（即2^0）。

1.1.1.3 二进制转八进制和十六进制

将二进制转换为八进制，可以将二进制数每三位分一组，从最低位开始，不足三位的高位补0，然后将每组转换为对应的八进制数即可。例如，将10001001转换为八进制：

10 001 001
 2  1  1
= 211

因此，10001001的二进制表示为211（八进制）。

将二进制转换为十六进制，可以将二进制数每四位分一组，从最低位开始，不足四位的高位补0，然后将每组转换为对应的十六进制数即可。例如，将10001001转换为十六进制：

1000 1001
 8    9

因此，10001001的二进制表示为89（十六进制）。

1.1.2 原码反码补码移码

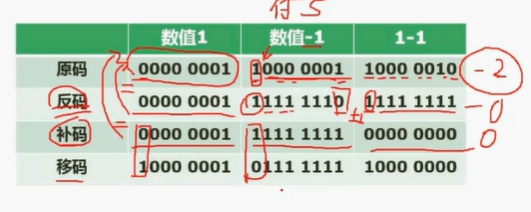
1.1.2.1原码

原码是一种最简单、最直观的二进制数表示法。在原码中，一个数用其二进制数绝对值的码位和符号位表示。其中，最高位是符号位，0表示正数，1表示负数。

例如，+7的原码为00000111，-7的原码为10000111。

1.1.2.2反码

反码是为了解决原码减法的问题而引入的，可以将减法运算转换成加法运算，从而简化计算机的硬件电路。在反码中，正数的反码与原码相同，负数的反码是其原码除符号位外各位取反。

例如，+7的反码为00000111，-7的反码为11111000。

1.1.2.3 补码

补码是为了解决反码的问题而引入的，可以将减法运算再次转换成加法运算，同时只有一个零表示方法，使用起来更加方便。在补码中，正数的补码与原码相同，负数的补码是其绝对值的二进制表示按位取反再加1。

例如，+7的补码为00000111，-7的补码为11111101。

1.1.2.4 移码

移码是对补码的符号位取反

例如，+7的补码为 00000111，-7的补码为 11111101。

+7的移码为 10000111，-7的移码为 01111101。

移码是为了方便浮点数的表示而引入的，通过将阶码与一个偏移量相加，可以将浮点数表示成一个固定长度的二进制数，方便进行计算和存储。在移码中，阶码用无符号整数表示，偏移量是2^(k-1)-1，其中k是移码的位数。例如，在32位移码中，偏移量是127，所以一个浮点数的移码等于其阶码加上127。

在计算机硬件电路中，使用补码比原码、反码更为普遍，而浮点数通常采用移码表示。

1.1.2.5 取值范围

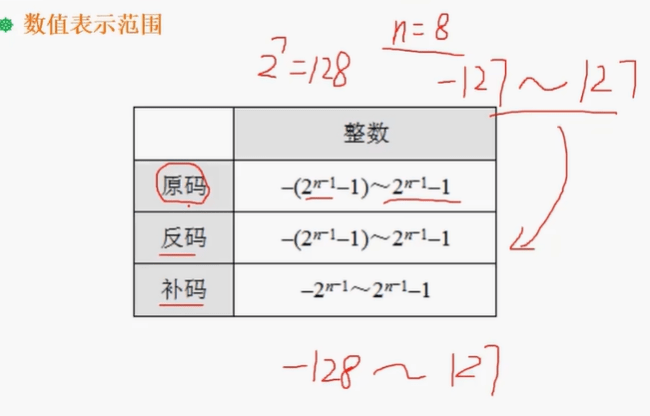
1681805005774

1.1.3 浮点数运算

多在选择题

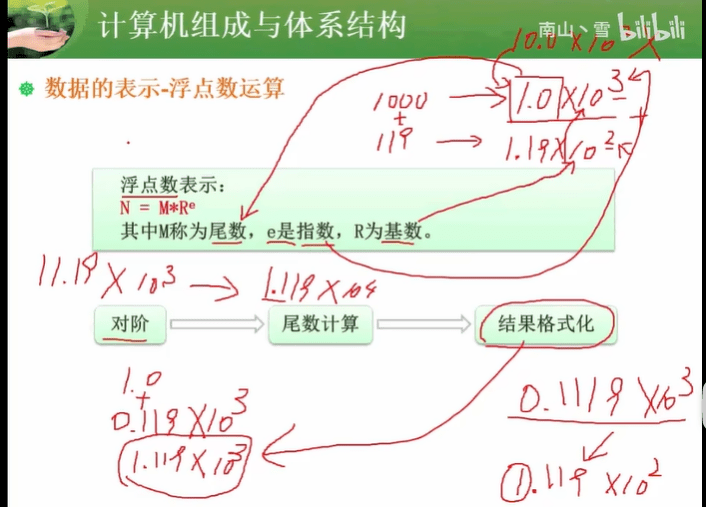
1681805237641

对操作数进行规范化，即将小数点左右移动，使小数部分最高位为1。
将小数点对齐，即将小数点位置相同。
对尾数进行运算，例如加法或乘法。
对结果进行规范化，即将小数点左右移动，使小数部分最高位为1。
如果结果超出了浮点数的表示范围，则进行舍入操作，将结果近似为最接近的浮点数。

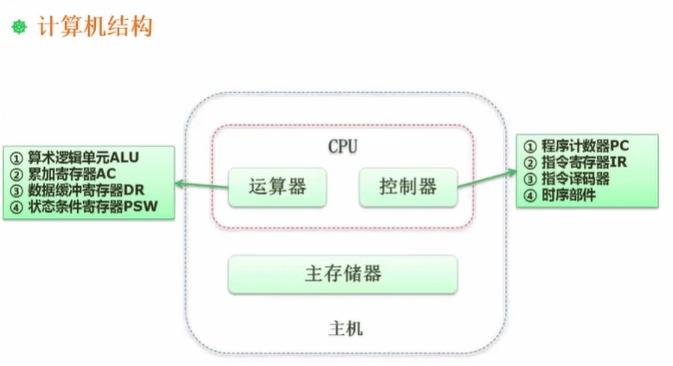
1.2 cpu结构

1681805795843

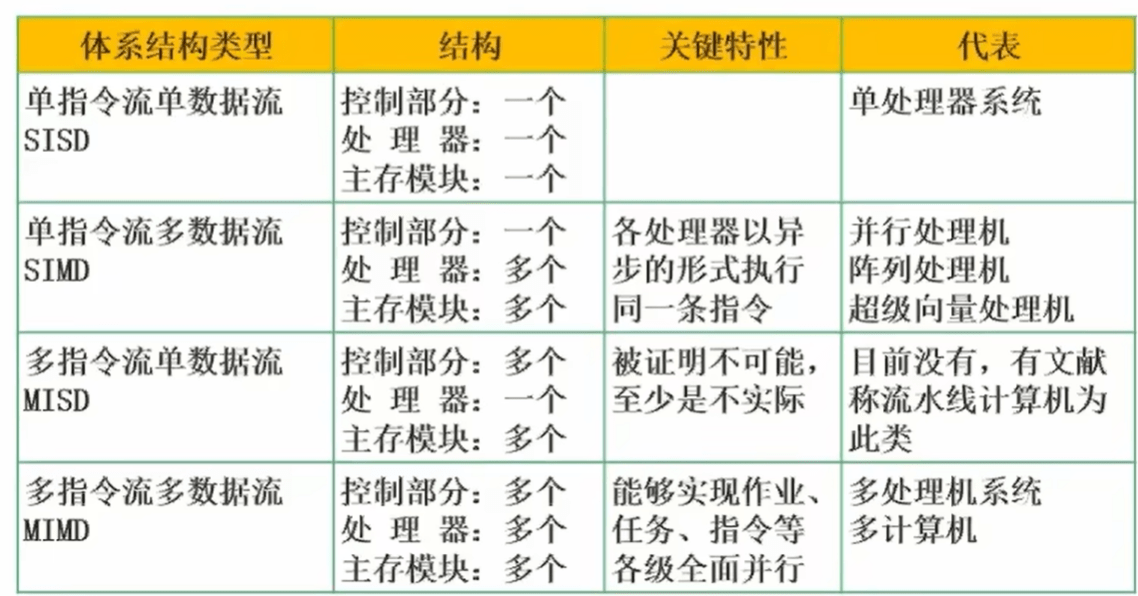
1.3 Flynn

1681807126963

1.4 CISC(复杂指令集)和RISC(精简指令集)

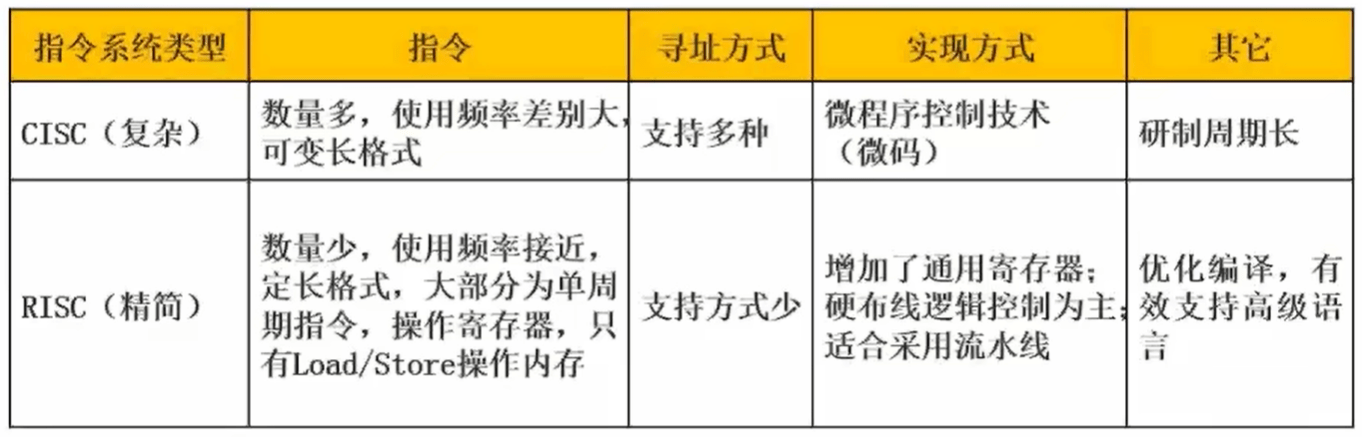
1681807078627

CISC和RISC指令集在设计思想、特点和使用场景方面有很大的不同。

设计思想：

CISC指令集的设计思想是将各种复杂的操作封装成单个指令，从而实现一种指令多功能的设计，以便于程序员编写复杂的程序。

RISC指令集的设计思想则是将指令集设计得更加简洁明了，以尽可能提高处理器执行指令的效率。

特点：

CISC指令集的特点是指令集非常复杂，包含了各种寻址方式、分支和子程序调用等操作，这些操作可以用单个指令来完成。CISC指令集还可以通过采用微指令控制器等技术来扩展指令集功能。CISC指令集的优点是能够简化编写代码的过程，但同时也存在指令执行效率低下的问题。

RISC指令集的特点是指令集设计相对简单，指令流水线化比较容易，因此可以提高指令的执行效率。RISC指令集的设计通常包含定长指令格式，使用寄存器作为操作数，而不是直接操作内存，这也有助于提高指令执行效率。但是，RISC指令集也因其指令集设计简单而无法完成复杂的操作，需要执行更多的指令。

使用场景：

CISC指令集适用于需要完成较为复杂的操作，如字符串处理、带有变长参数的子程序调用等应用场景。目前大部分PC计算机都采用的是x86系列处理器，这些处理器采用的就是CISC指令集。

RISC指令集则适用于需要大量执行简单操作的应用场景，如通信、图像处理、音频处理等。在嵌入式系统领域，RISC指令集也得到了广泛的应用，例如ARM、MIPS等处理器就采用了RISC指令集架构。

1.5 流水线

1.5.1 概念

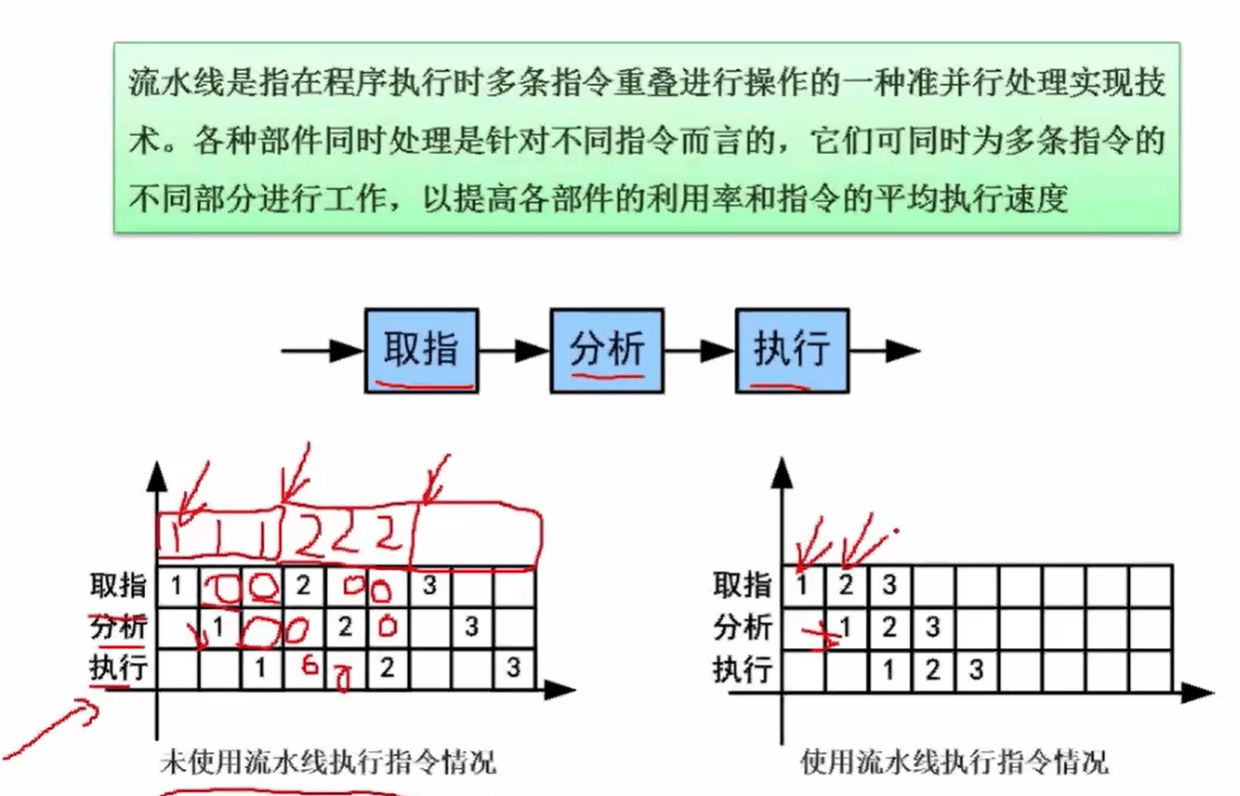
流水线概念

具体来说，处理器的流水线包括多个阶段，每个阶段完成特定的任务，各个阶段之间串联起来形成一个流水线，每个时钟周期处理器执行一个指令，并且每个阶段都在执行不同的指令。这样就可以同时完成多个指令的处理，提高处理器的整体性能。

1.5.2 流水线周期、执行时间计算公式

周期、执行时间计算公式

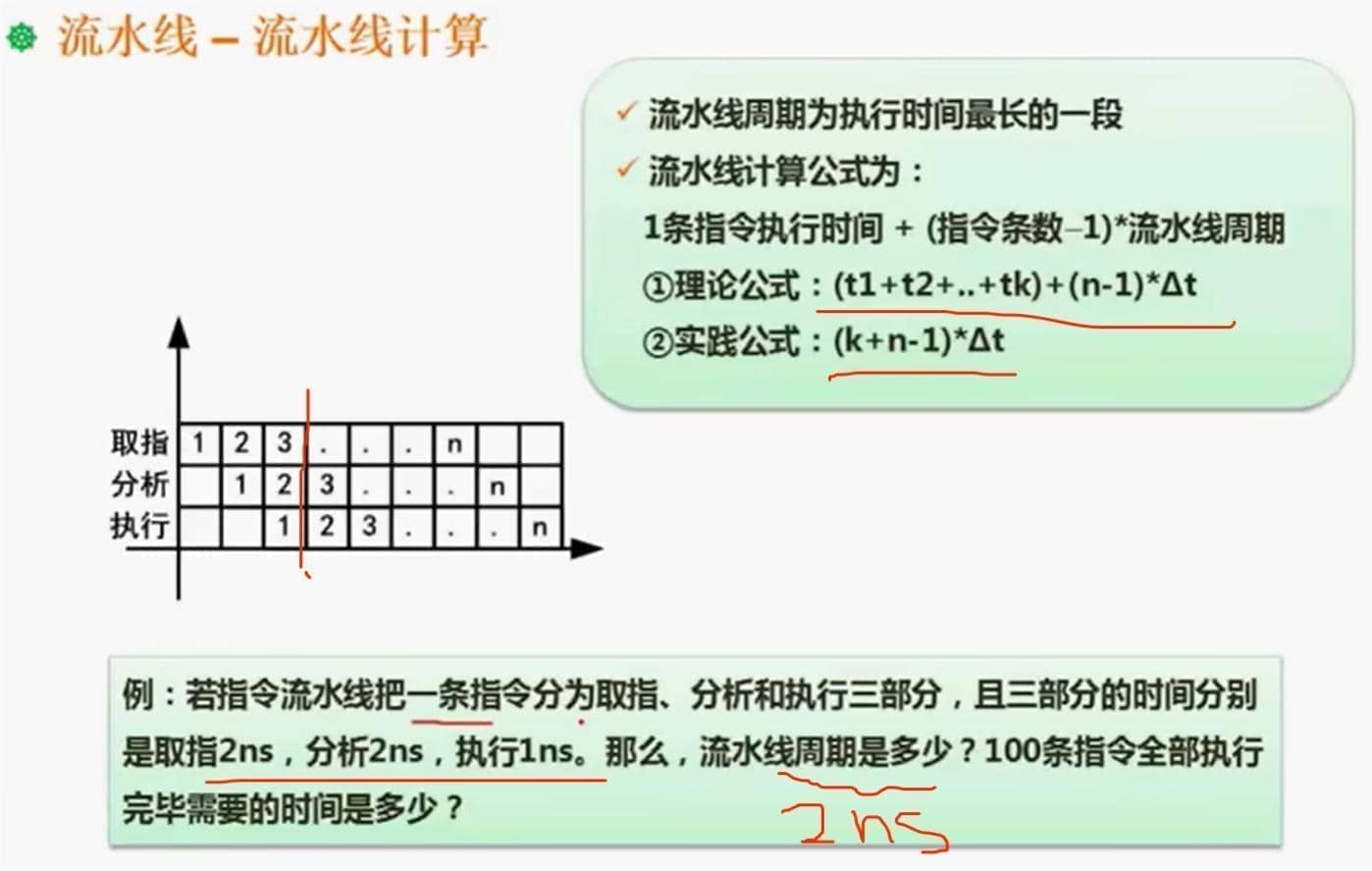
周期：最长的执行时间

执行一次流水线后就算正式开始，那么执行的时间就是

（第一次执行时间）+（n-1）*周期  
= (2+2+1) + (100-1) * 2
= 5 + 99 * 2   （括号内的减号可以看成是乘以-1）
= 5 + 198
= 203

实际上可能会把第一次执行的时间用周期来计算

（第一次执行时间）+（n-1）*周期  
= (2+2+2) + (100-1) * 2
= 5 + 99 * 2   （括号内的减号可以看成是乘以-1）
= 5 + 198
= 204

1.5.3 流水线吞吐率计算

吞吐率 = 指令条数/流水线执行时间
      = 100/203
      ≈ 0.4926

1.5.4 加速比和效率的技术

1.5.4.1 加速比

加速比 = 不使用流水线时间 / 使用流水线时间
= (2 + 2 + 1) * (100 / 1) / ((2 + 2 + 1) + (100 - 1) * 2)
 = 151 / 203 ≈ 0.7438
根据该公式，可得：
加速比 = 151 / 203 ≈ 0.7438
即使用流水线相较于不使用流水线可以将执行时间缩短约 25.62%，加速比为 0.7438。

1.5.4.2 效率

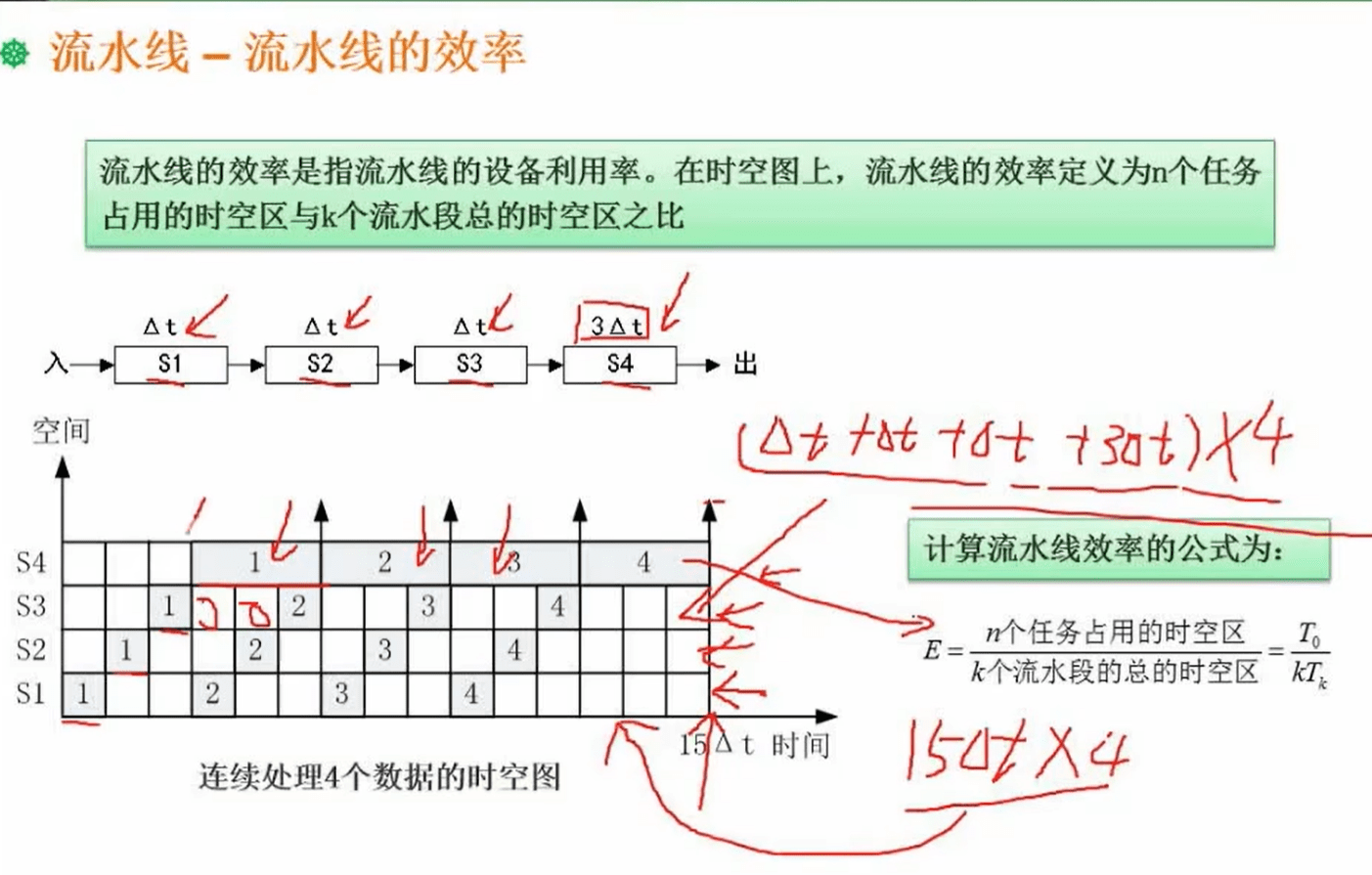
流水线效率

            也就是表格中灰色部分 / 总表格的大小
流水线效率 = n个任务占用的时空区总数 / k个流水段的总时空区
          = (t+t+t+3t) * 4 / 15t * 4 
其实就是计算灰格子占总表格的比例情况，比例越高效率越高

1.6 层次化存储结构

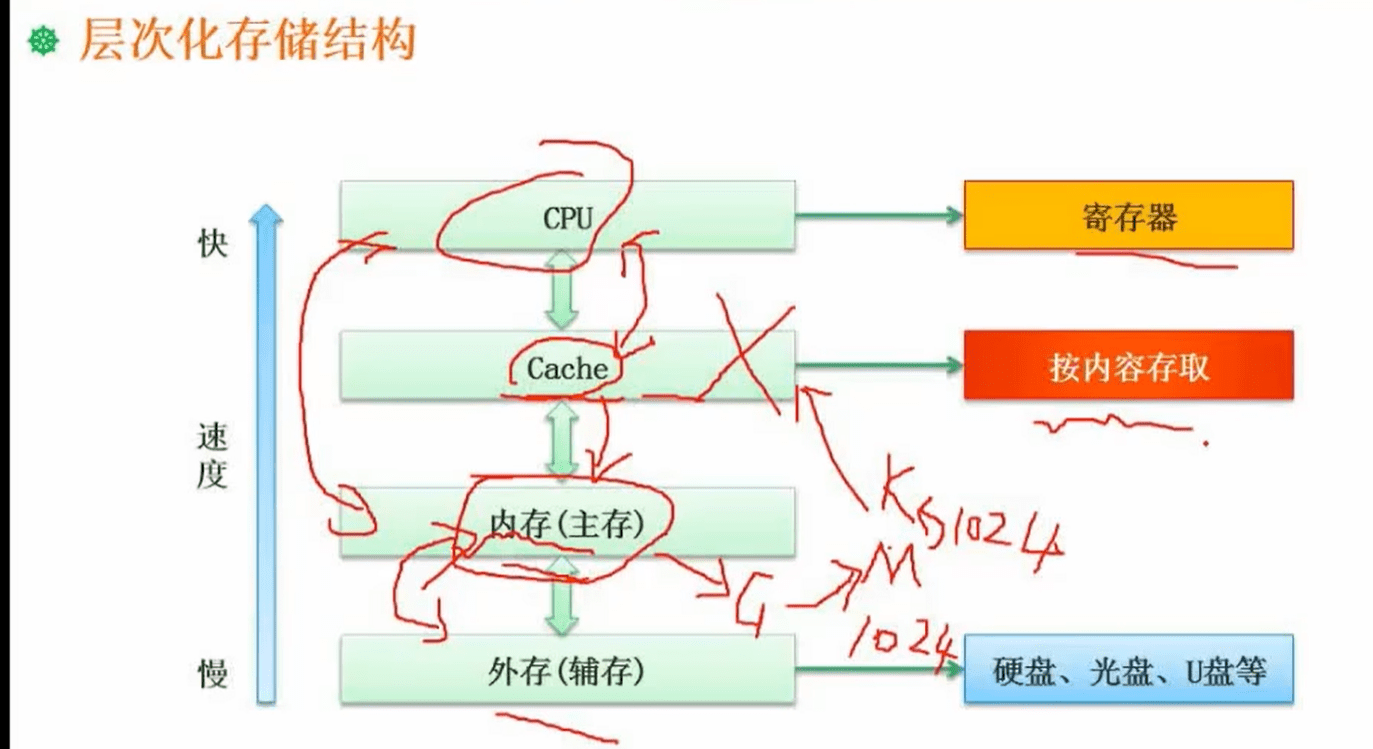
1682045420740

层次化存储结构是一种常用的计算机存储管理方式，将存储设备按照速度和容量等方面的不同进行分类，并建立多个层次之间的联系，实现信息访问和管理的高效性和可靠性。

例如，我们通常使用的计算机存储设备包括硬盘、光盘、U盘、固态硬盘等。它们在速度、容量、价格等方面存在差异，可以按照这些差异分为不同的层次，如主存、二级缓存、硬盘等。在这个过程中，每个层次都作为下一个层次的“容器”，并对其进行管理。

通过层次化存储结构，我们可以使计算机系统更加高效地利用存储资源，优化程序访问和存取数据的速度，同时提高系统的可靠性和安全性。

1.7 Cache的概念,周期计算公式

1682045848564

cache很多情况下用来做循环，避免重复从内存拿数据

计算存取周期:

假设访问cache需要 1ns ，访问内存需要 1000ns ，那么如果没有cache 存取周期就是 1000ns，而只使用 Cache 存取周期就是 1ns.

而如果 cache 和内存混用，假设 cpu 对 cache的访问命中率为 h(95%) 也就是有 5% 的几率需要去内存拿数据，那么就可以计算使用 cache 和内存混用的存取周期：

根据公式 t3 = h * t1 + (1-h) * t2，将 t1 替换为 1， t2 替换为 1000，h 替换为 0.95，可得：

t3 = 0.95 * 1 + (1-0.95) * 1000
= 0.95 * 1 + 0.05 * 1000
= 0.95 + 50
= 50.95 （保留两位小数）

因此，根据所给公式，当 h=0.95，t1=1，t2=1000 时，经过计算，t3 的值为 50.95。

1.8 局部性原理

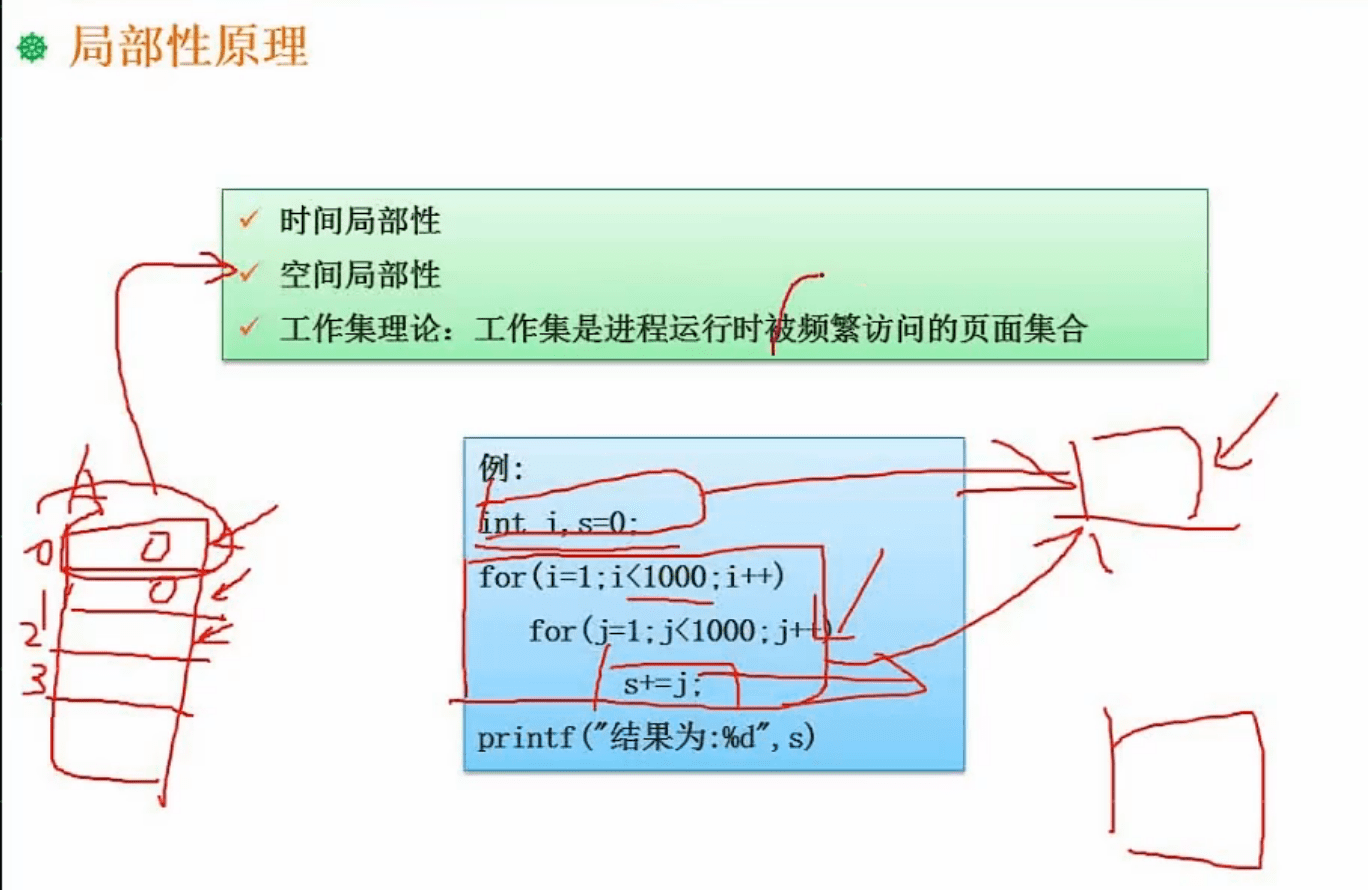
1682046813703

局部性原理是指在程序执行期间，数据和指令的访问倾向于集中在一定的空间范围内。具体来说，局部性原理包括以下两种：

时间局部性：指一个数据或指令在一段时间内可能被多次访问。这种情况下，就可以利用缓存等技术，将其存储在高速存储器中，以提高访问速度。（例：cache中的循环）
空间局部性：指一个数据或指令的访问往往与其周围的数据或指令有关联。这种情况下，就可以通过预取、预读等技术，将其附近的数据或指令也提前读取到高速存储器中，以提高后续访问的效率。（例：数组，空间都是临近的）
在使用工作集原理时，计算机系统会根据当前程序的访问模式，将其需要的数据和指令加载到内存和缓存中。当程序对数据和指令的访问发生变化时，系统会相应地调整工作集，加入新的数据和指令，或者删除不再需要的数据和指令。（例：把需要频繁访问内容打包一次拿过来，访问的时候就不用频繁调取）

1.9 主存的分类、编址

1.9.1 主存的分类

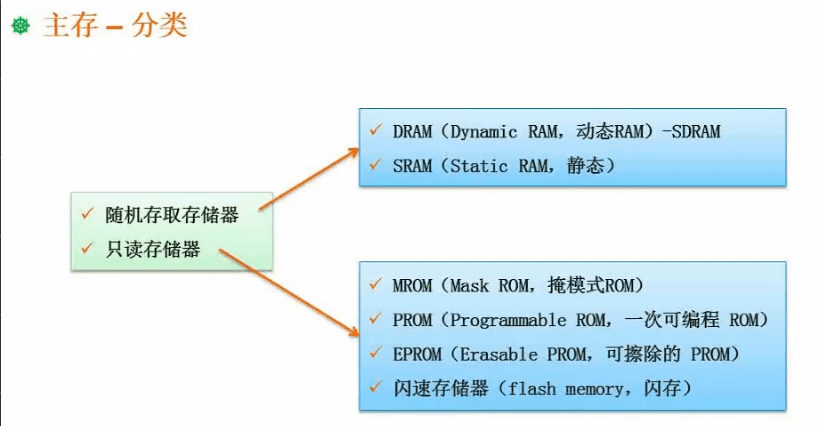
1682048392552

RAM（Random Access Memory）和 ROM（Read Only Memory）都属于计算机内存的范畴。它们都是用来存储数据和程序的硬件设备，在计算机中发挥着重要的作用。

RAM通常指的是随机访问存储器，是一种易失性存储器，意味着电源关闭后其中存储的数据会丢失。在 RAM 中，数据可以任意读写，并且存储器中的地址单元和存储单元可以动态地分配和释放，因此 RAM 也被称为“易失性随机存储器”（Volatile Random-access Memory）。 RAM 分为静态 RAM（SRAM）和动态 RAM（DRAM）两种，其中 SRAM 的速度比 DRAM 更快，但成本更高。

ROM通常指的是只读存储器，是一种非易失性存储器，其中存储的数据无法进行修改或删除。在 ROM 中，数据是预先写入并固化在芯片中的，因此它也被称为只读存储器（Read-only Memory）。在计算机中，ROM 通常用来存储固件或者操作系统等重要数据，以确保其不会丢失或被篡改。（例如 BIOS 就在rom中）

1.9.2 主存-编址

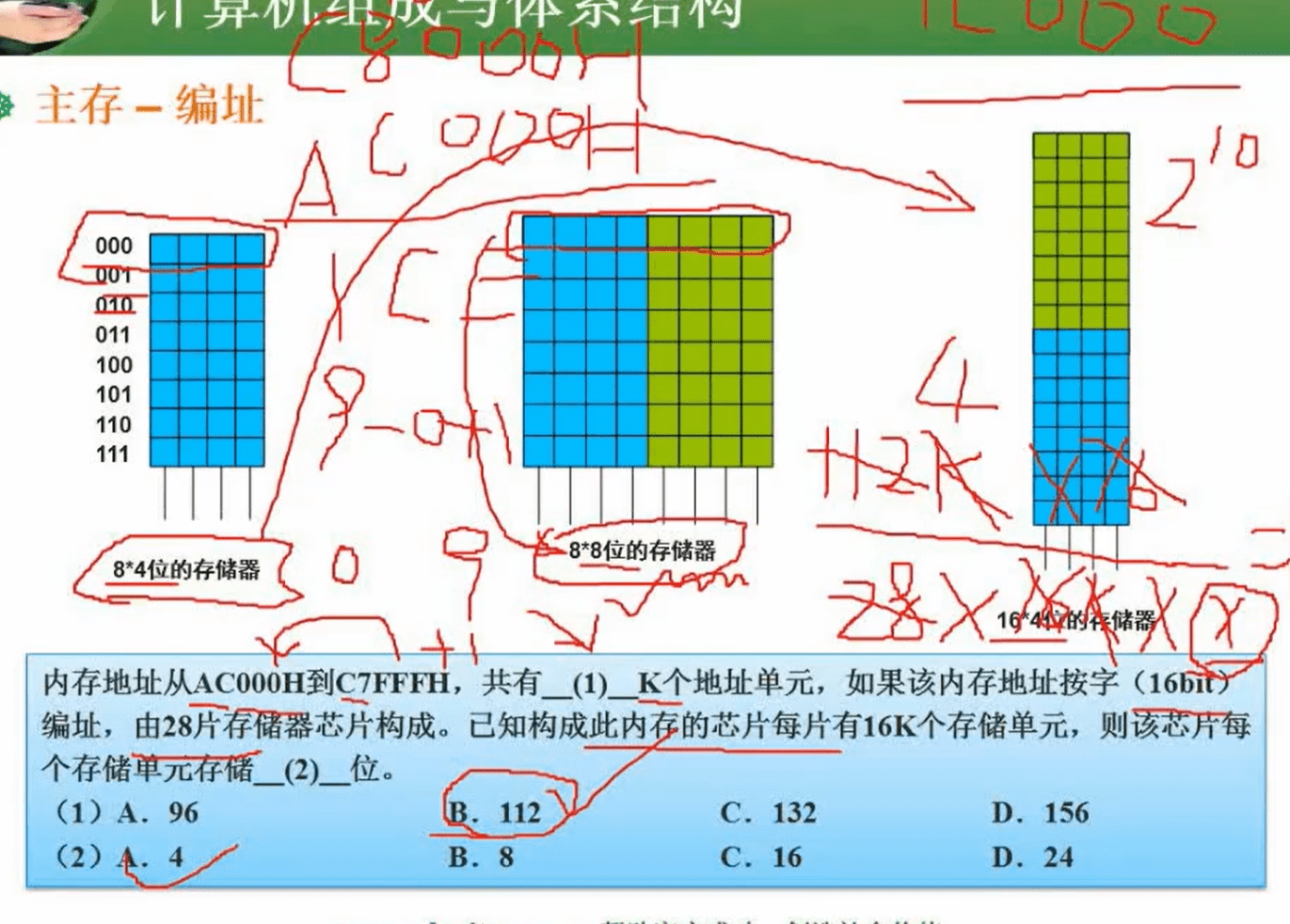
1683613501687

todo 不太明白

1.10 磁盘工作原理

1.10.1 磁盘结构和参数

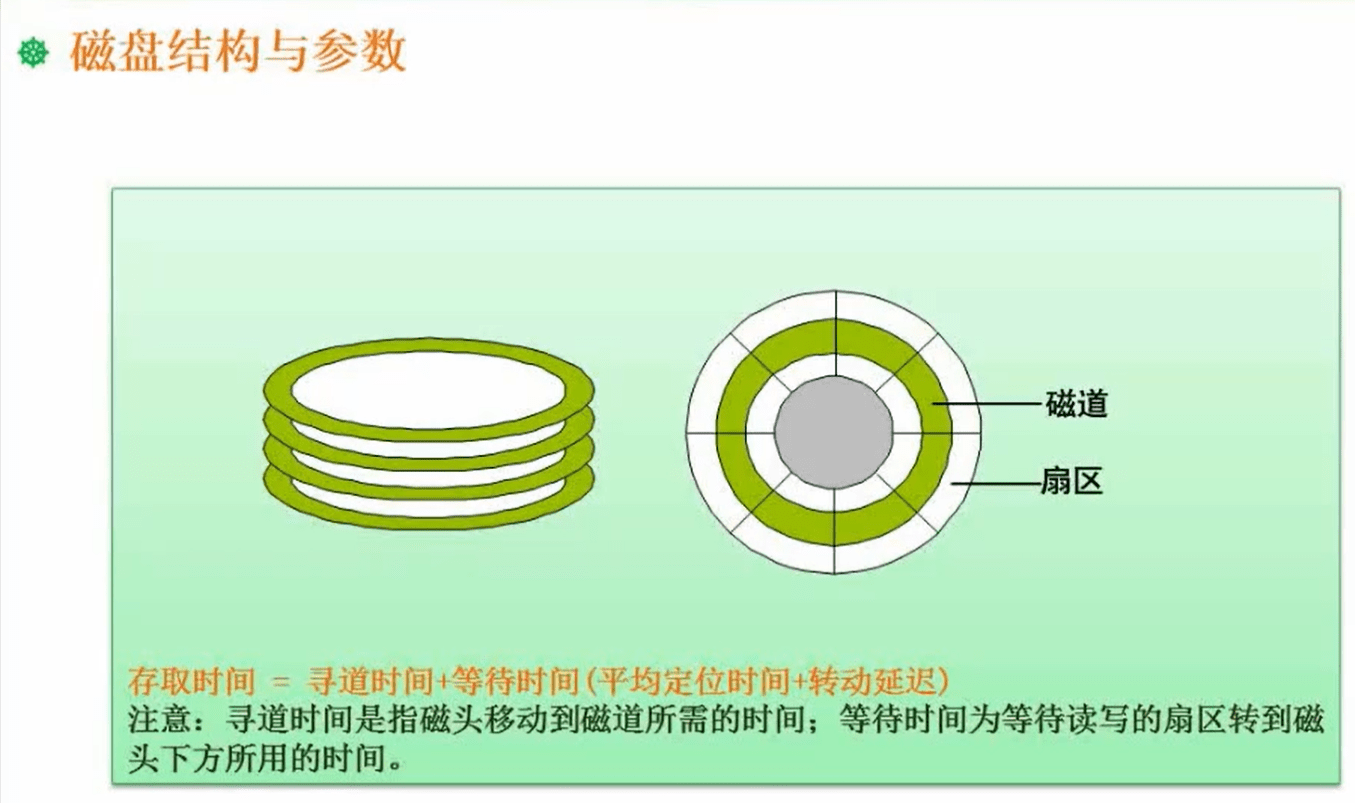
1683614304444

1.10.2 试题

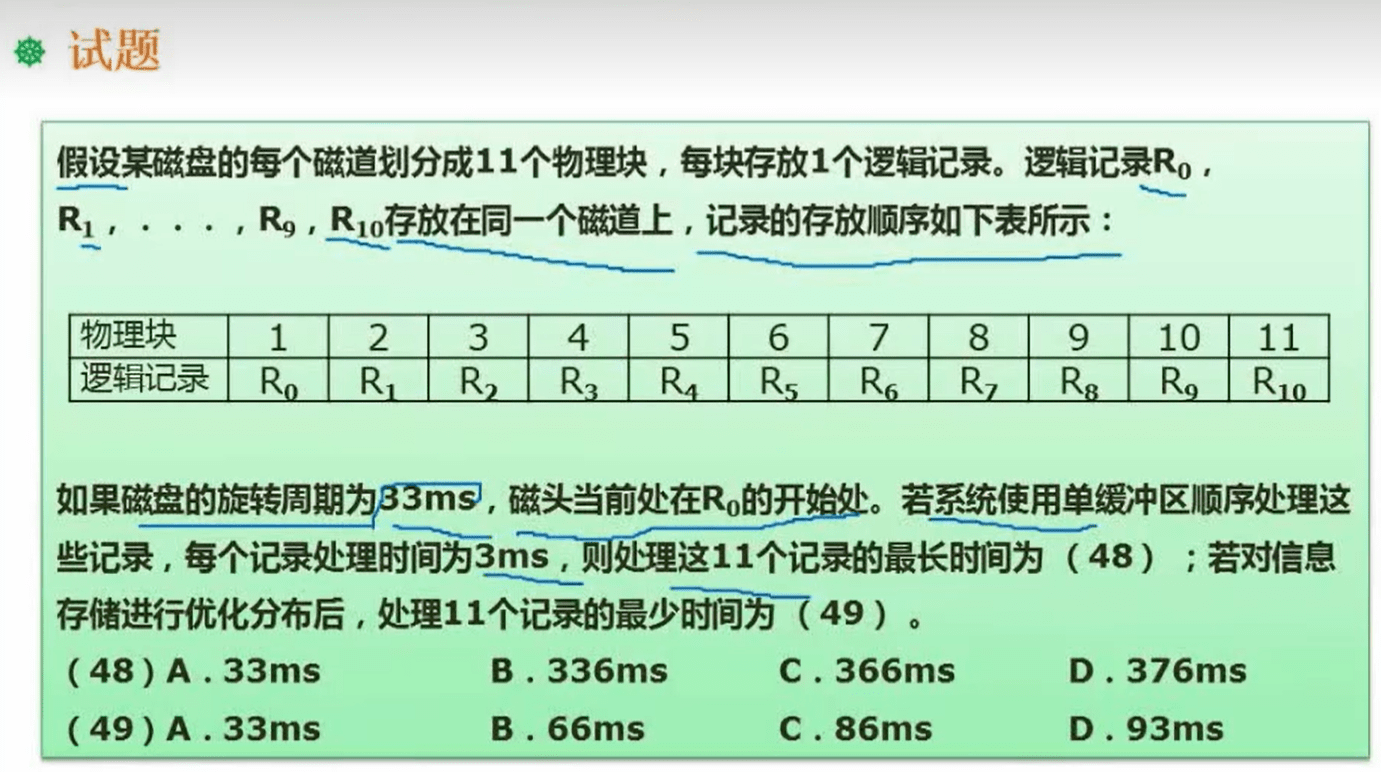
1683614422913

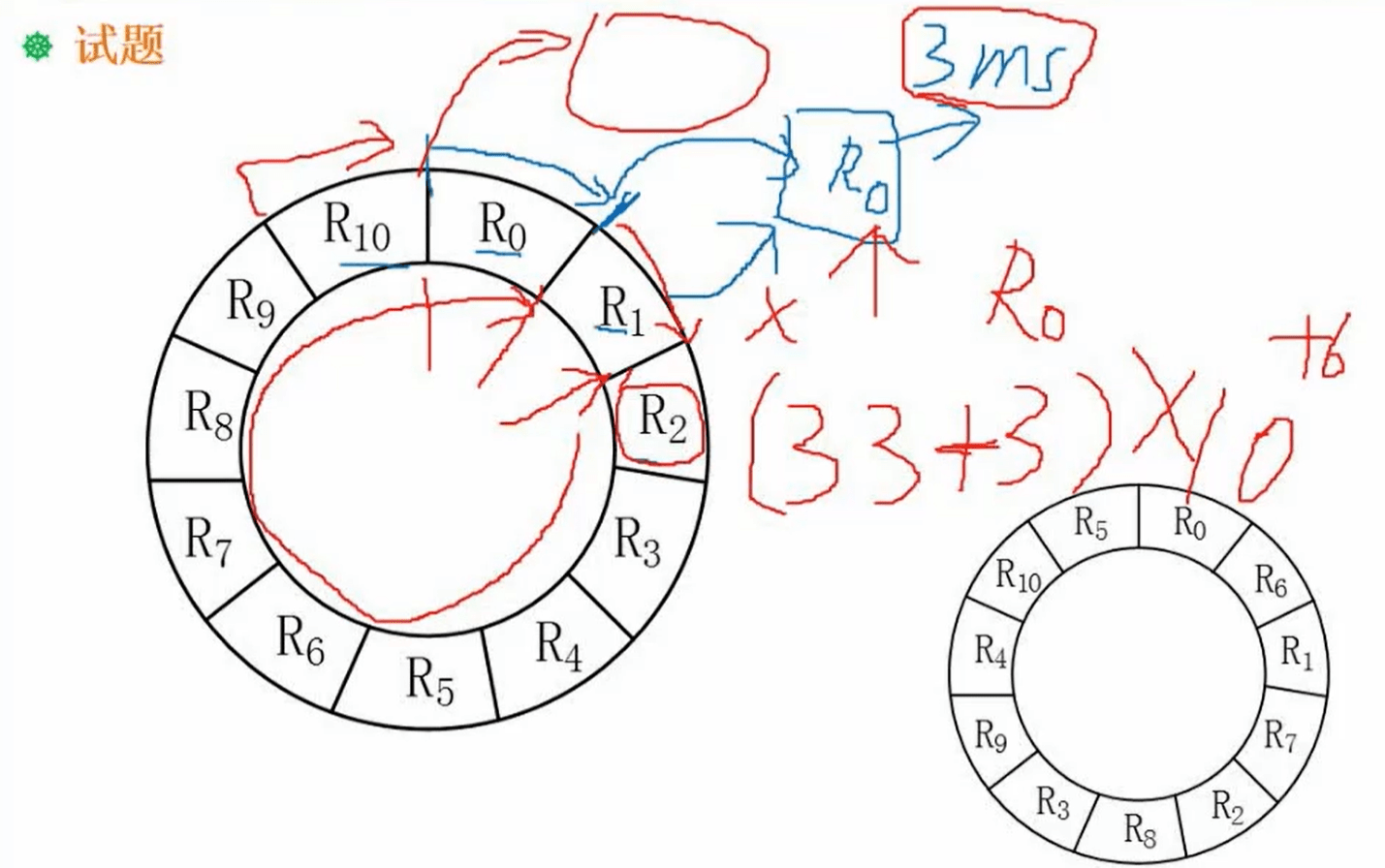
分析：一个11个物理块，周期 33 ms 也就是读取一个物理块3 ms，并且是单缓存区顺序处理，也就是读取数据后丢到缓存区去处理还需要3ms，并且只能顺序处理，那么按照下图：

1、从 R0 开始位置开始到 R0 结束，读取后丢到缓冲区，再等 3ms 处理

2、此时磁头已经到了 R2 的开始位置了，但是 R1 还没读取，所以要跑一圈跑到 R1 开始位置（33ms + 3ms）

3、R1 的读取和 R0 一致，一直到 R9 也读完，此时已经读了 10次了，所以时间是（33ms + 3ms）*10

4、R10 的读取到 R1 开始结束也就是再加 1个物理块 3ms 和 1个处理时间 3ms

所以公式：（33ms + 3ms）* 10 + 6 = 366

第二个空分析：

1、可以存储优化也就是不用按顺序存储，那么就可以隔一段进行存储，刚好避过读取时间和处理时间，也就是右下角的图的方式存储，处理情况就是需要跑两圈，第一圈处理 R0 到 R5 第二圈 R6 到 R10 ，也就是 33ms *2 = 66ms

1683614487573

1.11 总线

1683615556744

考察点：选择题

1.12 系统可靠性分析-串联系统与并联系统

1.12.1 串联系统与并联系统

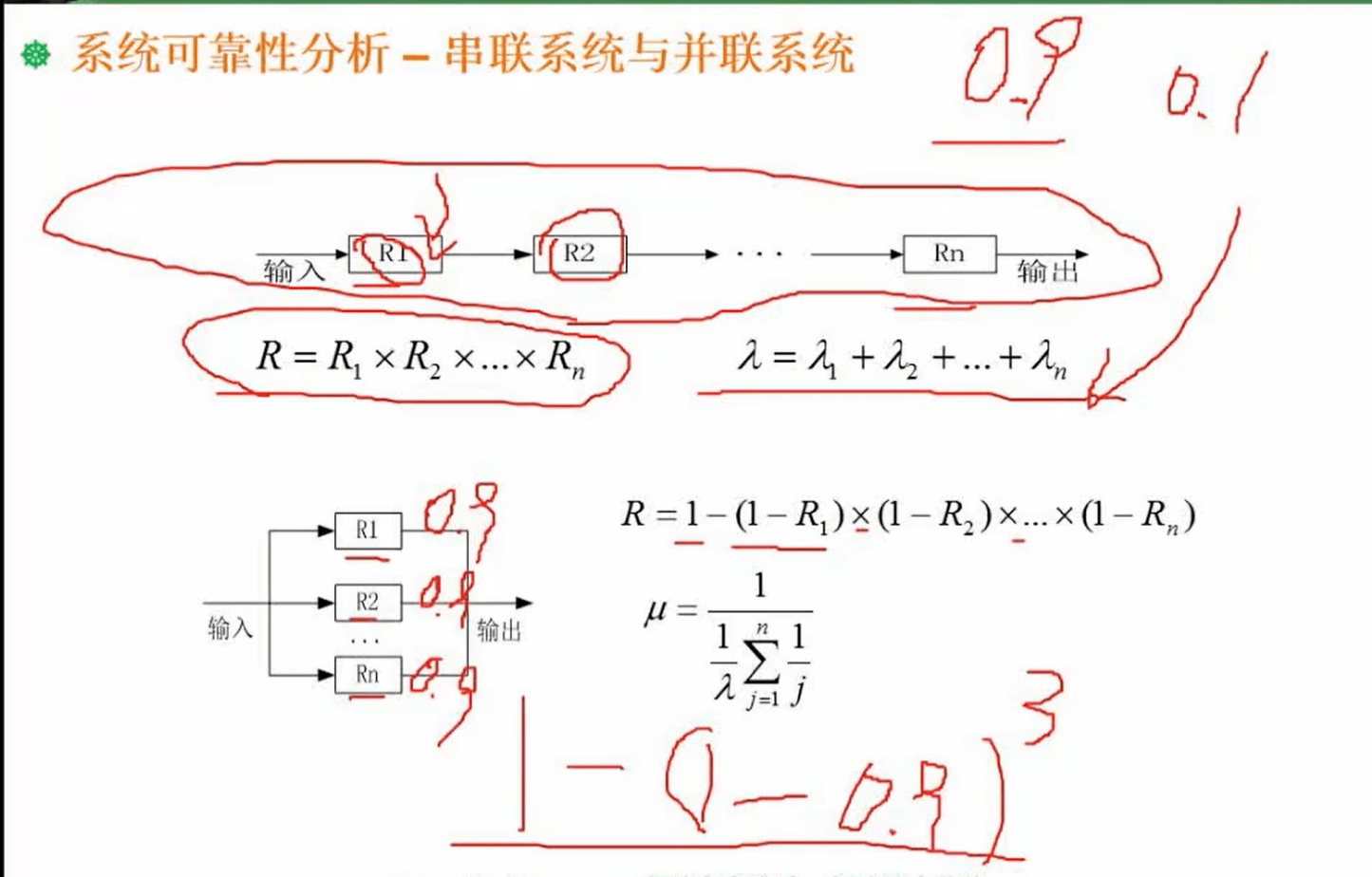
1683616062493

分析：

R 为可靠性

1、串联：只要有一个系统失效就失效，所以总体可靠性为 R1 * R2 * R3 … = R ,失效率就是 1 - R

2、并联：只有所有系统同时失效才算失效，所有先算失效率，再用 1- 失效率 = 可考虑，

1.12.2 串并联系统计算

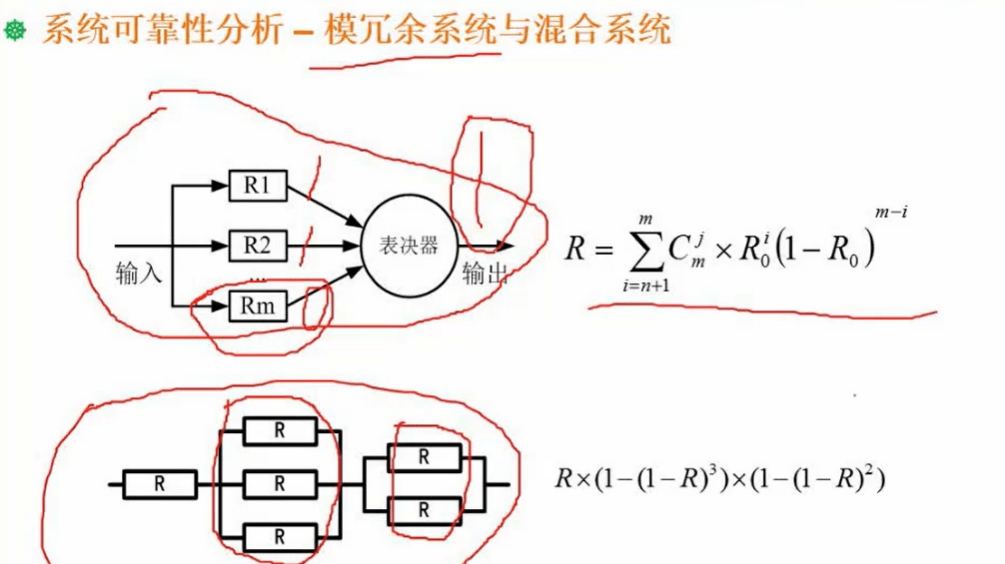
1683616414871

分析：

上面的一般不考。

下面串联并联一起的，先看总体是串联，所以是把各个整体的可靠性算出来再相乘

1.13 差错控制

1.13.1 海明校验码

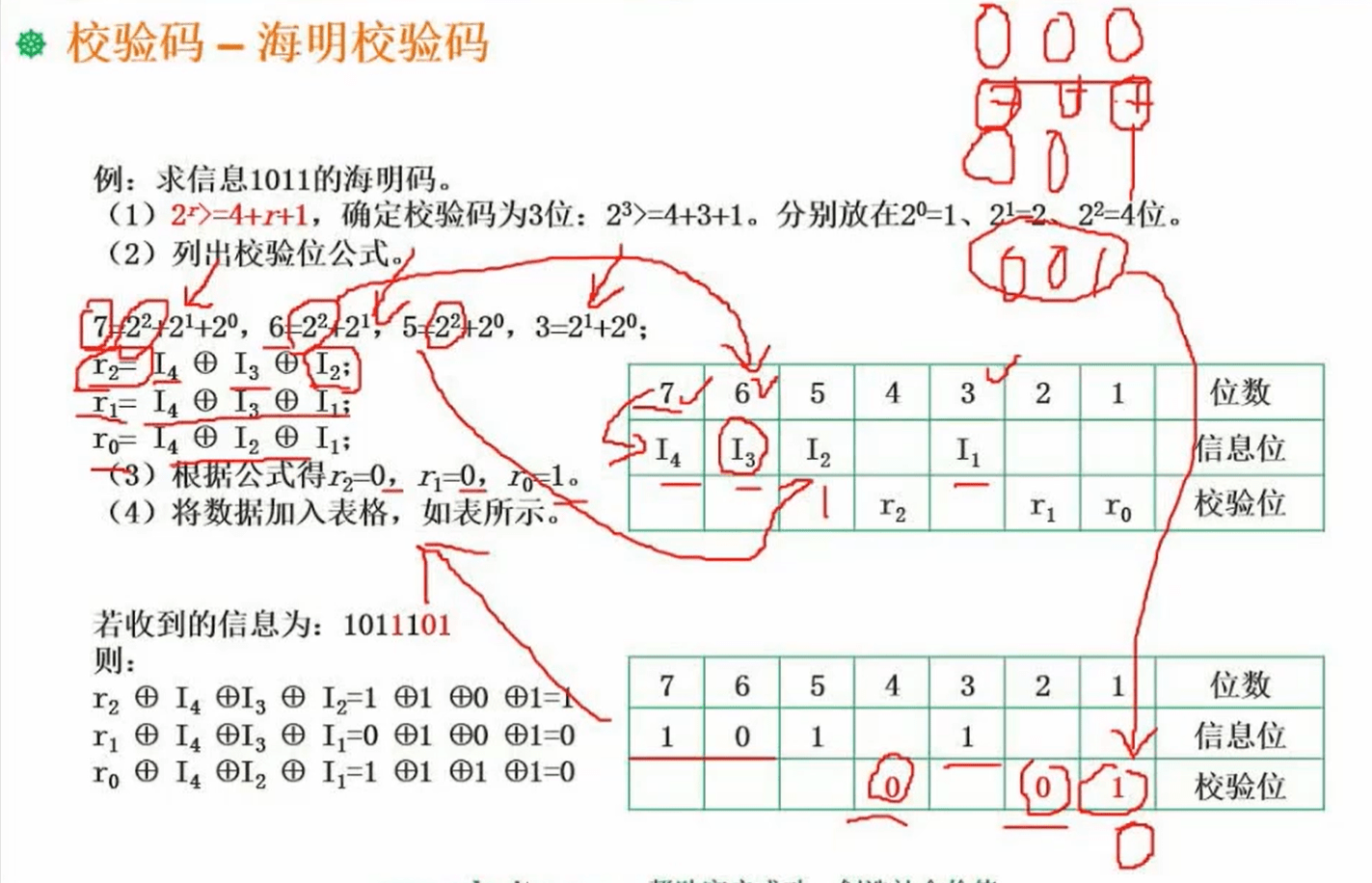
确定校验码有多少位

根据公式：2^r >= 信息位数+r+1

2^r >= 4 + r + 1

得到：r = 3，所以校验位：2^2 ,2^1 , 2^0

信息位化为二进制，涉及到的次方数就是对应校验位的异或内容，可以算出对应校验位的值，再带入表格，可以得到海明码： 1010101 。
纠错：比如如果收到的信息是：1011101 ，则我们根据收到的信息算校验码：

r2 = I4 ^ I3 ^ I2 = 1^0^1 = 0

r1 = I4 ^ I3 ^ I1 = 1^0^1 = 0

r0 = I4 ^ I2 ^ I1 = 1^1^1 = 1

计算的校验码：001

收到的校验码：101

校验码不同，则做异或：

得到100，也就是 100 位置上的值是错的，也就是第四位错了，做取反：1011101 -> 1010101

link

https://hikers.gitee.io/2023/04/18/ji-suan-ji-zu-cheng-yu-ti-xi-jie-gou/

本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 link !

软考计算机组成与体系结构

2.操作系统基本原理

2023-05-09 软考

软考操作系统基本原理

【PostgreSQL】记一次少数据量的表（1w内）但查询缓慢的问题

2023-04-12 postgresql 性能优化

postgresql sql

1.计算机组成与体系结构

计算机组成与体系

1.1 数据的表示

1.1.1、进制转换

1.1.1.2、二进制转十进制

1.1.1.2 十进制转二进制

1.1.1.3 二进制转八进制和十六进制

1.1.2 原码 反码 补码 移码

1.1.2.1原码

1.1.2.2反码

1.1.2.3 补码

1.1.2.4 移码

1.1.2.5 取值范围

1.1.3 浮点数运算

1.2 cpu结构

1.3 Flynn

1.4 CISC(复杂指令集)和RISC(精简指令集)

1.5 流水线

1.5.1 概念

1.5.2 流水线周期、执行时间计算公式

1.5.3 流水线吞吐率计算

1.5.4 加速比和效率的技术

1.5.4.1 加速比

1.5.4.2 效率

1.6 层次化存储结构

1.7 Cache的概念,周期计算公式

1.8 局部性原理

1.9 主存的分类、编址

1.9.1 主存的分类

1.9.2 主存-编址

1.10 磁盘工作原理

1.10.1 磁盘结构和参数

1.10.2 试题

1.11 总线

1.12 系统可靠性分析-串联系统与并联系统

1.12.1 串联系统与并联系统

1.12.2 串并联系统计算

1.13 差错控制

1.13.1 海明校验码

1.1.2 原码反码补码移码